Recently developed methodologies have made great progress in fitting a complicated shape of spatial distribution and handling large spatial data. I have studied contemporary statistical models and computational algorithms for analyzing large spatial point-referenced data, and proposed a Bayesian Markov-Chain-Monte-Carlo covariance modeling of a spatially structured process over a two-dimensional rectangular lattice grid in view of the Fourier spectral density approach Jun and Lim (2021). As a natural extension of this idea, we also proposed a novel time series regression and applications to forecast foreign exchange rate data Jun, Lim, and Kim (2022).
Spatial Statistics has already been brought into the mainstream of statistical research, and it will continuously play an important role in statistical modeling in data-centric applications. In particular, there is an apparent demand for enriching and exploiting methodologies to deal with computational and practical challenges from large spatiotemporal datasets with high dimensional settings. I have special expertise in this research direction in joint work with great mentors (Dr. Chae Young Lim, Dr. Zhengyuan Zhu). I also have abundant experience in GIS-data processing, graphical visualization, and software package developments designed for spatial data analysis.
Nonparametric Spectral Bayesian Spatial Regression
Paper link : Jun and Lim (2021)
Github link : NSBSR
Abstract :
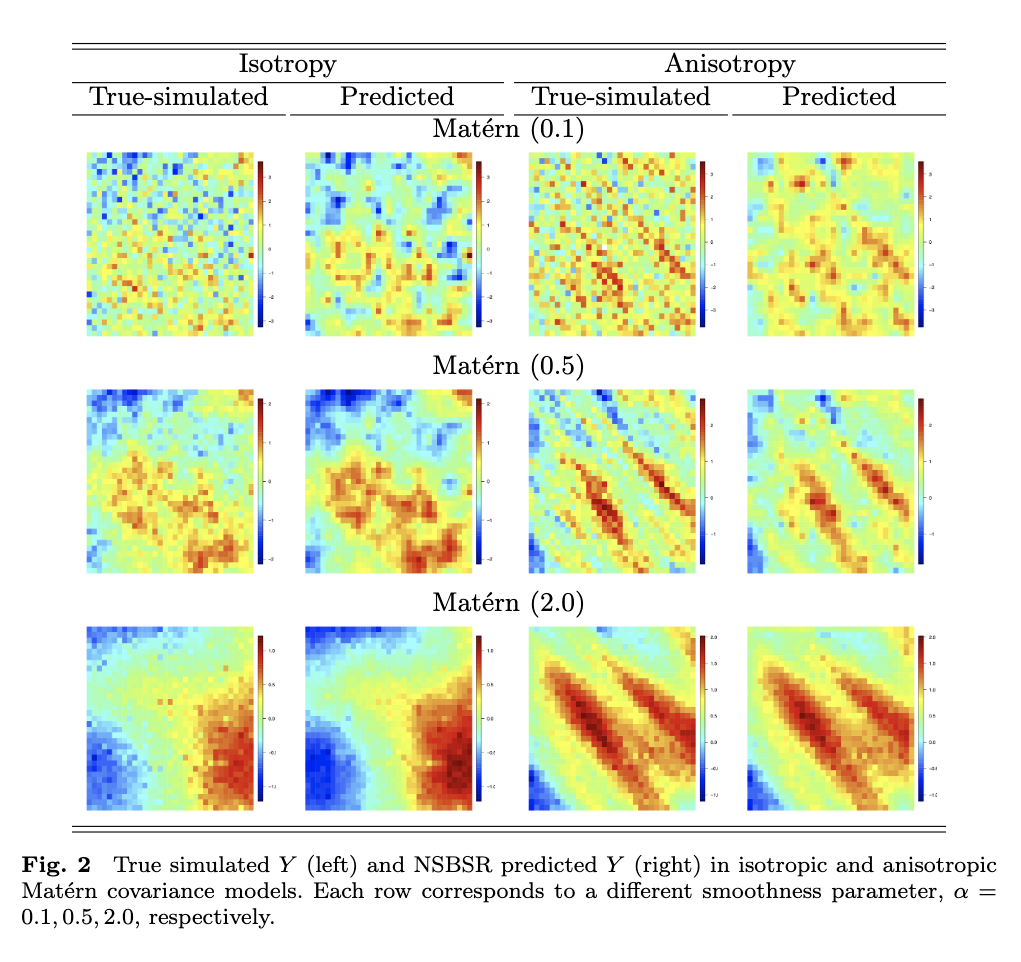
We consider modeling of Fourier coefficients, known as a spectral density function to represent spatial dependence of a stationary spatial random field and use it for spatial regression under a Bayesian framework. Especially, we switch from the space domain to the frequency domain and introduce a Gaussian process prior to the log spectral density. As we do not impose any further assumption on log spectral density, resulting covariance function is not of a parametric form and/or isotropic assumption. Simulation study supports that our approach is robust over various parametric covariance models. Also, our approach gives comparable or better prediction results over conventional spatial prediction under most parametric covariance models that we considered. Even though we need to estimate spectral density at all Fourier frequencies during the Bayesian procedure, our approach does not lose much computational efficiency compared to estimating only a few parameters in the parametric covariance models. We also compare our approach with some other existing spatial prediction approaches using two datasets of Korean ozone concentration. Our approach performs reasonably good in terms of mean absolute error and root mean squared error.
Nonparametric Spectral Bayesian Temporal Regression
Paper link : Jun, Lim, and Kim (2022); Jun, Kim, Kim, and Lim (2025+)
Github link : NSBTR
Abstract :
Autocovariance of the error term in a time series model plays a key role in the estimation and inference for the model that it belongs to. Typically, some arbitrary parametric structure is assumed upon the error to simplify the estimation, which inevitably introduces potential model-misspecification. We thus conduct nonparametric estimation of it. To avoid the difficult bandwidth selection issue under the traditional nonparametric truncation approach, this paper conducts the Bayesian estimation of its spectral density in a frequency domain. To this end, we consider two cases: fixed error variance and time-varying one. Each approach is taken to estimate the spectral density of the autocovariance and the model parameters. The methodology is applied to exchange rate forecasting and proves to compete favorably against some benchmark models, including the random walk without drift.